Bonne année
et merci à "JLM" pour ses dessins !

Introduction
Cette deuxième partie portera essentiellement sur l'algèbre. Il s'agit d'un nouveau "moment" dans l'histoire des mathématiques : alors que jusqu'ici on traitait les problèmes à partir du connu pour aller vers l'inconnu (en géométrie essentiellement), l'invention de l'algèbre va consister essentiellement à prendre en compte l'inconnu(e) comme matériau de travail.
On débutera avec la période VIIIème-IXème siècle et cela nous mènera jusqu'à l'aube de la révolution scientifique du XVIIème siècle, avec comme d'habitude des incursions dans les mathématiques récentes.
Il va falloir se familiariser avec un nouveau paradigme, des méthodes et un langage entièrement différents de ceux de la géométrie.
Le contexte géopolitique
Localisations
du VIIIe au milieu du XIIe siècle : l’Âge d'or islamique
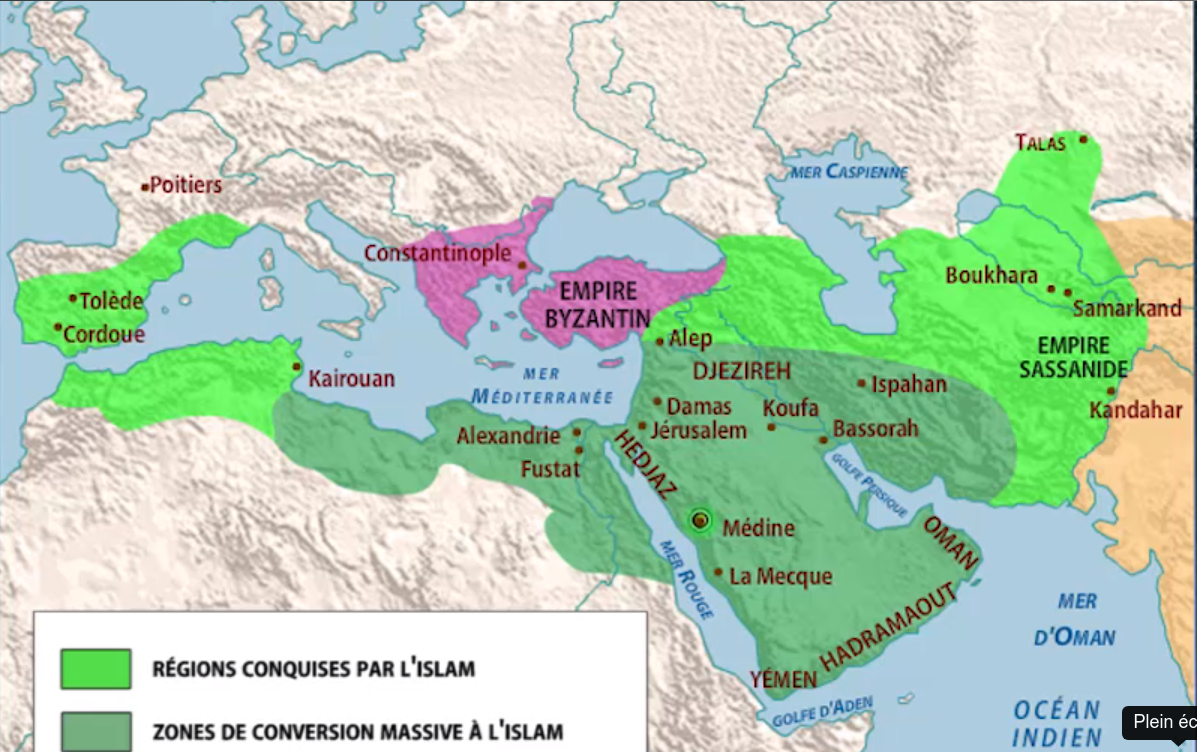
du XIIème siècle au XVIème siècle : la Renaissance en Occident

Extensions
- l'empire arabe prend le contrôle politique des territoires byzantins (Damas - 635 - Omeyyades) et en particulier égyptiens (Alexandrie en 640) anciennement hellénisés
- puis de la Perse (Bagdad - VIIIème s - Abbassides) où s'étaient exilés de nombreux savants grecs après la fermeture de l'école néoplatonicienne d'Athènes par Justinien en 529
Héritages
- les savants arabes se forment au contact des savants chrétiens et juifs qui habitaient ces régions
- ils s'y trouvent aussi en contact avec les civilisations indienne et chinoise.
- traductions en arabe accompagnées de lectures critiques des ouvrages de l'Antiquité en physique, mathématique, astronomie et médecine
Les "Maisons de la Sagesse"
Bagdad devint la capitale intellectuelle de son époque. Des écoles et des bibliothèques furent construites. Al-Mamun, calife de 813 à 833, avait réuni à Bagdad des savants de tous horizons.

Apports moyen-orientaux
Tradition algorithmique orale ? : la question de l'écriture cunéiforme

Importance de la langue arabe
« Les langues sémitiques tendent à la formation abrégée et abstraite, “algébrisante”, des idées. » [Louis Massignon]
« La conception de la science qu’a engagée le linguiste al-Khalîl comme la méthode qui l’accompagne sont deux conditions de possibilité de l’algèbre d’al-Khawârizmî. » [Roshdi Rashed]
- une langue "combinatoire" : système trilatère
- exemple de la Perse qui ne produit pas de math avant la domination arabo-musulmane
Retour sur Diophante
problème (degré 1)
On partage un héritage de 105 drachmes entre 3 enfants ; le premier reçoit le double du deuxième, le deuxième reçoit 5 drachmes de plus que le troisième
solution algorithmique
- retranche 15 drachmes de l'héritage : tu obtiens 90
- divise 90 en 4 parts égales : tu obtiens 22 drachmes et demi (c'est la part du troisième)
- ajoute 5 à cette part : tu obtiens 27 drachmes et demi (c'est la part du deuxième)
- multiplie cette part par 2 : tu obtiens 55 drachmes (c'est la part du troisième)
solution géométrique
Diophante (héritage)
On représente la part du troisième par le segment AB
AB + (AB + 5) + 2(AB + 5) = 105 (mise en équation géométrique)
4 AB + 15 = 105
4 AB = 90
AB = 22.5 part du troisième
A'B' = 27.5 part du deuxième
A"B" = 55 part du premier
problème (degré 2 à une inconnue)
Soit un rectangle dont l'aire est 187 et dont la longueur mesure 6 unités de plus que la largeur
solution algorithmique
- divise l'excédent (6) par 2 : tu obtiens 3
- élève ce nombre au carré : tu obtiens 9
- ajoute ce résultat à l'aire (187) : tu obtiens 196
- prends la racine du nombre obtenu : soit 14
- retranche lui le résultat (3) de la première étape : tu obtiens 11 qui est la largeur cherchée
- ajoute l'excédent (6) pour obtenir la longueur : 17
solution géométrique
Diophante : détermination d'un rectangle
On représente la largeur par le segment AB
AB(AB+6) = 187
A² + 6AB = 187 (figure)
(AB + 3)² - 9 = 187
(AB + 3)² = 196
AB + 3 = 14
AB = 11
problème (degré 2 à une inconnue et un paramètre)
somme de 2 carrés
Décomposer un carré (rationnel) en somme de deux carrés (rationnels)

Al-Khwarizmi
Présentation
Le mot algorithme est dérivé de son nom
Le mot algèbre est dérivé du titre d'un de ses livres

Généralités
L'apport fondamental d'Al-Khwarizmi est la constitution de l'algèbre comme discipline : alors que des pratiques algébriques existaient bien avant lui aussi bien en Grèce qu'en Mésopotamie, en Inde et en Chine par exemple, il va aborder d'une manière générale :
- la question de l'inconnue
- la question de la classification à priori des équations (caractère combinatoire lié à la langue arabe)
Invention de l'algèbre
Le projet initial
L'invention de l'algèbre par Al-Khawârizmî vers 830 va survenir en réponse décalée à une commande étatique visant à mieux calculer les impôts, héritages et autres surfaces agricoles.
La réalisation
Al-Khawârizmî ne produit pas un traité de fiscalité mais le traité d'une nouvelle discipline mathématique qu'il décide d'appeler Livre de la réduction et de la comparaison - [ kitâb al-jabri wa al-muqâbalati ] - et ce n'est qu'ensuite qu'il va lui annexer un traité technique de calcul des transactions, des mensurations et des testaments.
al-jabr c'est la restauration bâti sur la racine jbr "rebouter, réparer" ; Don Quichotte tombé de cheval va voir l'"algébriste"
jabr : restaurer (ce qui manque), c'est à dire les "négatifs" (en terme actuel) : on les ajoute de chaque côté
puis muqabala, assmblage, regroupement des termes semblables dans chacun des membres
La nouveauté
L'invention de l'algèbre repose donc sur un pas de côté, sur un retrait par rapport à la commande étatique, geste négatif qui a pour contrepartie l'affirmation d'un nouveau type de confiance spécifiquement mathématique en un nouveau type de rationalité fait de décisions fondatrices, de déductions et de démonstrations, de calculs et d'algorithmes, type qui va bien vite appeler un nom propre spécifique : précisément celui d'algèbre, prélevé dans le titre même du traité d’Al-Khawârizmî.
Les points importants
Dans l'algèbre on va accepter de travailler directement avec l'inconnu(e) alors que jusqu'ici on allait du connu à l'inconnu. Les calculs qui se faisaient sur des nombres connus dans les algorithmes ou sur des grandeurs connues en géométrie vont être étendus à des quantités inconnues.
De plus ceci va permettre de dépasser les problèmes conceptuels rencontrés (par Diophante par exemple) lorsqu'il fallait additionner des longueurs et des surfaces.
Les chiffres indiens
Une partie de son travail est un cours "algorithmique" de calcul avec les chiffres indiens (Kit ab al-jam'wal tafriq bi hisab al-Hind - Livre sur l'addition et la soustraction d'après la méthode des Indiens). On peut déjà voir dans la structure du système décimal un embryon de ce qui sera au cœur de l'algèbre : le zéro qui marque une place vide (l'inconnue) mais qu'on doit expliciter, les calculs sur les puissances de 10 qui s'expriment comme des expressions algébriques.

L'algèbre
Un exemple
énoncé
Un carré plus 10 racines sont égaux à 39 dirhams
Vocabulaire utilisée :
- la racine est l'inconnue (ce qu'il faut trouver)
- la carré est le carré de cette racine
- les dirhams sont les constantes
procédé
- partage en deux moitiés le nombre des racines : il vient 5
- que tu multiplies par lui-même : il vient 25
- tu l'ajoutes à 39 : on aura 64
- tu prends la racine : qui est 8
- de laquelle tu soustrais la moitié du nombre des racines : il reste 3
- qui est la racine du carré que tu veux, le carré étant 9
"la cause"
Une démonstration par la géométrie, "à la Diophante"
un carré plus 10 racines sont égaux à 39 dirhams puis généralisation
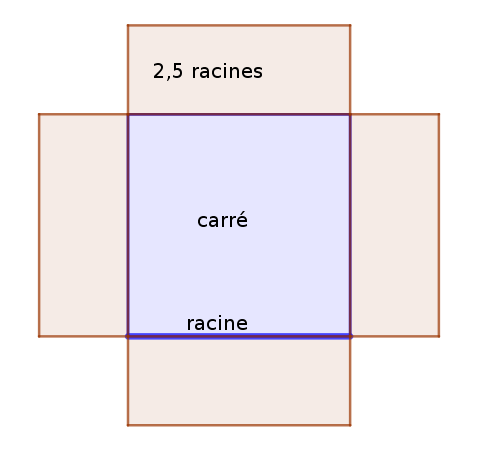
La classification des équations du second degré
La langue de l'algèbre
l'algèbre arabe ne connaissait pas encore le calcul algébrique littéral. Il se faisait dans la langue vernaculaire ordinaire, dans l'arabe littéraire de l'époque. Mais l'esprit algébrique était déjà là : le calcul algébrique qu'on effectuera plus tard « à la lettre » était alors phrasé c'est-à-dire projeté dans la langue vernaculaire. Ceci se faisait avec des mots venant nommer l'inconnue par des mots (racine jizrun ou chose chay’un), non par des lettres.
La classification
Comme à cette époque on n'utilise pas de nombres négatifs ni le zéro (même s'il vient d'être introduit) on doit distinguer plusieurs cas
Les trois équations simples puis les trois équations combinées d'al-Khawârizmî se phrasent ainsi :
- « \(bx = c\) » se dit : “Des racines sont égales à un nombre”
- « \(ax² = c\) » se dit : “Des carrés sont égaux à un nombre”
- « \(ax^2 = bx\) » se dit : “Des carrés sont égaux à des racines”
- « \(ax^2²+bx = c\) » se dit : “Des carrés et des racines sont égaux à un nombre”
- « \(ax^2²+c = bx\) » se dit : “Des carrés et un nombre sont égaux à des racines"
- « \(bx+c = ax^2\) » se dit : “Des racines et un nombre sont égaux à des carrés"
Y-a-t'il d'autres cas ? : début de la combinatoire
La résolution des équations
celles qui se ramènent au premier degré
Pour chacun des cas la méthode (généralisée) d'Al-Khwarizmi donne une formule pour la racine
- On peut voir l'équation \(bx = c\) de plusieurs manières : comme un problème de partage (si \(b\) est un entier), comme une simplification par \(b\), ou comme la relation entre la multiplication et la division.
- On peut ramener ce cas au précédent en raisonnant sur \(x^2\) comme sur \(x\)
- \(ax^2=bx\) s'écrit \(axx=bx\) et en simplifiant par \(x\) (cas 1) on obtient \(ax=b\) ce qui se ramène encore au cas 1. Autre méthode : en simplifiant par \(a\) (cas 1) on se ramène à un carré de côté \(x\) égal à un rectangle de côtés \(\frac{b}{a}\) et \(x\)
celles qui ne se ramènent pas au premier degré
- On simplifie par \(a\) ce qui donne la forme \(x^2+Bx = C\) et "on répartit les \(Bx\) autour du carré \(x^2\)"
- On simplifie par \(a\) ce qui donne la forme \(x^2+C = Bx\) puis on raisonne comme ci-dessus en enlevant au carré de côté \(x\) quatre "coins carrés" de côtés \(\frac{B}{4}\)
- On simplifie par \(a\) et on procède comme ci-dessus
Les applications
calculs algébriques : formules pour les opérations sur les carrés, les fractions et les racines carrées
\((a \times b)^2=a^2 \times b^2\) ; \(\left(\frac{a}{b}\right)^2=\frac{a^2}{b^2}\)
\(\frac{a}{b}\times\frac{c}{d}=\frac{a \times c}{b \times d}\) ; \(\sqrt{a \times b}=\sqrt{a} \times \sqrt{b}\)
Attention : ces formules ne sont pas vraies pour l'addition et la soustraction
réponses aux questions du cours précédent
- la formule \(a \times 0 = 0\) n'est pas un axiome : elle se déduit de l'égalité \(a \times (1+0) = a \times 1 + a \times 0\) en développant à gauche et en simplifiant à droite du signe =.
On dit que 0 est un élément absorbant pour la multiplication. - plus généralement, à partir des "axiomes" des opérations on peut déduire certaines propriétés des opérations, par exemple :
pourquoi "moins par plus donne moins" :
(+2)×((+5) + (-5))
= (+2) × 0 = 0
= (+2) × (+5) + (+2) × (-5)
donc (+2) × (-5) = -(+2) × (+5) = -10
pourquoi \(a^0=1\) :
\(a^0 \times a^1 = a^{0+1}=a^1\)
problèmes se ramenant à des équations du premier et du second degré
- exemples
- Le calcul des héritages
- analogies avec le système décimal
Autres contributions des mathématiciens arabes
Combinatoire, "triangle de Pascal"
identités remarquables
- rappel : la combinatoire des consonnes dans la construction des racines
- développements de \((a+b)^2\), \((a+b)^3\), ... et construction du triangle arithmétique
remarque : le triangle de Pascal a été redécouvert par Pascal dans un conexte probabiliste, sans relation avec celui des arabes qui avait été construit, là aussi indépendamment dans un contexte combinatoire (calcul du nombre de racines trilatères possibles) puis algébrique (voir ci-dessous). De même il sera à nouveau redécouvert indépendamment par Newton dans un contexte algébrique.
identités remarquables et triangle d'Ibn Mun'im

commentaire
- Importance des problèmes techniques de calcul dans la construction de la rationalité : le développement de \((a+b)^4\) n'admet plus de figuration géométrique donc on passe à du calcul purement algébrique qui, lui, montre des "régularités" dans les coefficients du développement ce qui va amener à la nécessité pour la démonstration de la régularité d'inventer la démonstration par récurrence qui va elle-même devenir un instrument universel de démonstration.
- De plus le "triangle de Pascal" va être, dans les multiples interprétations qui vont en être faites, le germe de l'invention du calcul des probabilités (Pascal) et de l'analyse combinatoire par exemple : écriture sous forme d'un arbre, dénombrement, ...
Récurrence, analyse infinitésimale
calcul de la somme des entiers de 1 à n
On a déjà vu la formule : \(1+2+...+n=\frac{n(n+1)}{2}\)
démontrée par les mathématiciens grecs à l'aide du gnome ou encore par Gauss.
Les remarques faites par les mathématiciens arabes concernant la démonstration "par récurrence" permettant de construire le triangle de Pascal sont utilisables pour fournir une nouvelle démonstration de cette formule.
Si \(1+2+...+n=\frac{n(n+1)}{2}\) alors
\(1+2+...+n+(n+1)=\frac{n(n+1)}{2}+(n+1)=1+2+...+n+\frac{2(n+1)}{2} = \frac{(n+1)(n+2)}{2}\)
calcul de la somme des carrés des entiers de 1 à n
Une démonstration par récurrence permet d'établir l'égalité
\(1^2+2^2+3^2+ ... + n^2 = \frac{n(n+1)(2n+1)}{6}\)
Cette formule va permettre de calculer l'aire sous la parabole ce qui préfigure le calcul infinitésimal au XVIIème siècle
somme des carrés et aire sous la parabole
D'autres mathématiciens arabes
Al Haytham
Il affirme l’existence des objets mathématiques comme les lignes, les surfaces et les solides dans le domaine des idées, en faisant abstraction des objets concrets : ceux qui existent pour les sens n’existent pas en vérité car les sens trompent souvent sans que l’opérateur le décèle alors que ceux qui existent en imagination existent vraiment et absolument.
Omar Khayyam (1048-1131)
- le poète mathématicien : "Qui t’amène vive comme le vent pour attiser le feu déjà ardent en ton absence."
- évoque le problème des dimensions : "Et si l’algébriste emploie le carré-carré dans les problèmes de géométrie, c’est métaphoriquement, et non pas proprement, étant donné qu’il est impossible que le carré-carré fasse partie des grandeurs. Ce qui se trouve dans les grandeurs, c’est d’abord une seule dimension, c’est-à-dire la seule racine, ou, rapporté à son carré, le côté. Puis les deux dimensions, c’est-à-dire la surface... enfin les trois dimensions, c’est-à-dire le corps... comme il n’existe aucune autre dimension, ne font partie des grandeurs ni le carré-carré ni, à plus forte raison, ce qui lui est supérieur."
- classifie les équations du 3ème degré (en particulier pour essayer de résoudre le problème de la trisection de l'angle) : 25 cas dont 14 sont résolues géométriquement par intersection de coniques ; pour la solution algébrique des équations du troisième degré, Omar Khayyam dit : "elle n’est possible ni pour nous, ni pour aucun de ceux qui sont passés maîtres en cette science. Peut-être qu’un de ceux qui viendront après nous la réalisera."
Nasir al Din al Tusi (1201-1274)
Il classe les 25 cas d’Omar Khayyam suivant le nombre de leurs racines réelles positives.
Cherche le maximum d’un polynôme, introduit ce que nous reconnaissons être une dérivée et étudie le signe du polynôme au voisinage de ce point.
Ghiyath Al Kashi (autour de 1380-1430)
Mathématicien perse connu par sa formule de trigonométrie du triangle
\(a^2 = b^2+c^2-2 \times b \times c \times cos(A)\)
Développement de la trigonométrie à partir des connaissances grecques d'abord mais surtout indiennes.
trigonométrie et théorème d'Al Khashi
Transmission en Occident
Quelques considérations historiques
- au XIIIème siècle Avicenne par exemple est la base de l'enseignement à la fois dans les pays arabes et en Occident (Italie par exemple)
- déclin à partir du XIIàme - XIIIème siècle pour des raisons politiques (fragmentation de l'"empire" arabe) et religieuse
- pourquoi la future révolution scientifique va-t-elle se passer en Occident ? Est-ce dû au mode de production de la connaissance : universitaire en Occident mais pas dans les pays arabes ?
- la raison est commune à tous les hommes (Abélard XIIème siècle)
- les idées sont les passeurs (et non les hommes) : la mondialisation scientifique du Moyen Age est le fait des concepts
- il y a un espace commun immense avec une grande cohérence pour les modèles scientifiques (qui sont d'ailleurs faux du point de vue de la science moderne) ; ce n'est pas leur adéquation avec le réel et leur efficacité qui fait que ces concepts se maintiennent (ce qui va plutôt être le cas avec la future révolution scientifique), c'est parce qu'il y a une communauté de savoir et de pratique. - Continuum d'un "régime de scientificité" commun, d'une commensurabilité (référence à Thomas Kuhn) des discours scientifiques. [Joel Chandelier]
Les traductions
De la même façon que les arabes ont traduit très tôt les philosophes grecs (en particulier les Rhêtoriques d'Aristote) pour connaître la manière de pensée dans cette culture et donc pouvoir en débattre ou la combattre, la civilisation latine occidentale va traduire pour la même raison (en particulier en période de croisades) les textes arabes philosophiques (y compris le Coran) et scientifiques.
Deux écoles : (différence entre traduction et interprétation)
- traduction littérale (mot à mot) des textes religieux et par extension de tous les textes : ceci amène à des traductions directes du Grec au latin (à Pise, Antioche, ...) qui sont très diffciles à comprendre (Aristote en particulier)
- traduction selon le sens : pour les traductions arabo-latines des textes essentiellement scientifiques ou philosophiques il y a les deux écoles.
traduction d'Al Khwarizmi en latin

Gerbert d'Aurillac
Tentative de transmission des chiffres arabes qui échoue à cause de l'opposition de l'église pour des raisons "économiques", même si c'est le diable qui est invoqué.
L'algoriste contre l'abaciste

Léonard de Pise, dit Fibonacci (~1170 - ~1240)
En contact avec les arabes à Bougie (Bajaia en Algérie) pour sa collaboration dans les affaires de son père.
Il expose la numération décimale (Liber Abaci, 1202).
Dans ce livre apparaît la "suite de Fibonacci". Fibonacci
La diffusion de son œuvre est très restreinte à cette époque.